[고체역학] 보의 처짐, 보의 탄성 곡선 미분 방정식, 처짐 곡선 방정식 유도
1. 처짐 곡선 방정식
보에 횡하중이 작용하면 보의 축선은 구부러져 곡선으로 변형된다.
이 구부러진 중심선을 탄성 곡선 또는 처짐 곡선이라고 하며, 구부러지기 전의 중심선에서
이 탄성 곡선까지의 수직 변위를 처짐(Deflection)이라 한다.

곡선의 곡률은 순수 굽힘의 곡률과 굽힘 모멘트에 대한 관계식
(미소거리 ds 사이의 임의의 요소에 있어서는 순수 굽힘 가정)

으로 표현이 가능하다.
θ 는 x축 (가로) 과 M 점이 이루는 각도을 나타내며
dθ는 M과 N점에서의 그 곡선의 접선 또는 법선 사이의 각을 나타낸다.
미소거리 ds 와 곡률 반지름 ρ 사이의 관계식은 ds = ρ x dθ이며

로 표현이 가능하다.
탄성 영역내에서는 일반적인 보의 경우 지지점 사이의 거리에 비해 곡률이 작으므로

할 수 있으며

라고 할 수 있다.
여기서 아래의 tanθ 수식을 s에 대하여 미분하면


로 표현이 가능하다.
※ (참고) 아래의 수식 이용하여 미분 ----------------------------------------------------------------------------------------

(dy/dx) ^2 은 1에 비하여 매우 작은 값으로 무시할 수 있으며 따라서 아래와 같이 정의 가능.

-------------------------------------------------------------------------------------------------------------------------------------------
위의 유도된 방정식(수식2)를 (수식 1) 에 따라 정의 하면 아래와 같다
(절대값이 있어서 ± 를 붙인다)

위로 볼록한 곡선에서 dy/dx 는 x가 증가함에 따라 감소하고, 아래로 볼록한 곡선에서
dy/dx 는 x가 증가함에 따라 증가하므로 (수식3)는 M(굽힘모멘트)의 부호와 항상 반대임!
따라서
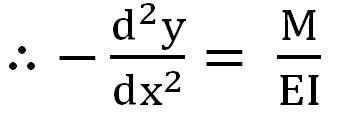
( 수식 4 ) 는 대칭면 내에서 굽힘 작용을 받는 보의 탄성 곡선의 미분 방정식 또는
처짐 곡선의 미분 방정식이 된다.
이를 이용하여 처짐각! 처짐량, 전단력 등의 식을 유도할 수 있다.