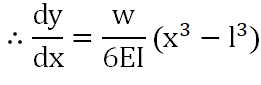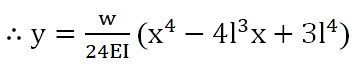[고체역학] 보의 처짐, 외팔보의 처짐, 처짐각, 처짐량 (집중하중, 분포하중)
[고체역학] 보의 처짐, 외팔보의 처짐, 처짐각, 처짐량 (집중하중, 분포하중)
1. 집중하중을 받는 외팔보의 처짐각, 처짐량
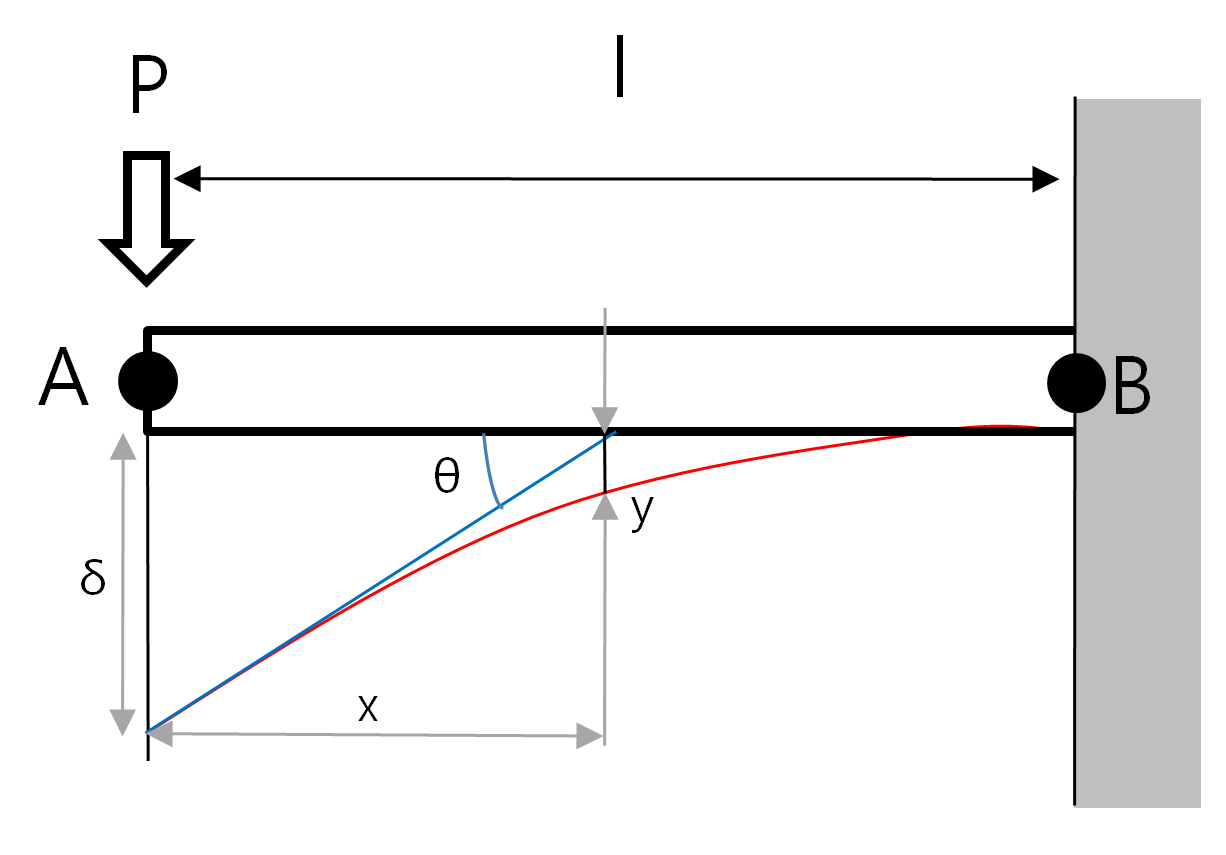
길이 l 인 외팔보의 자유단에 집중 하중 P를 받을 때의 처짐각과 처짐량에 대해 알아보겠다.
먼저 자유단으로 부터 x 거리에 있는 임의의 단면에서의 굽힘 모멘트 M 은
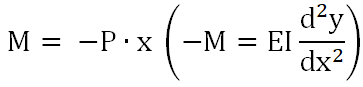
M에 대해서는 앞서 확인한 처짐 미분 방정식을 통해 확인 가능하다 (아래 글 참고)
2023.04.30 - [공학/고체역학] - [고체역학] 보의 처짐, 보의 탄성 곡선 미분 방정식, 처짐 곡선 방정식 유도
[고체역학] 보의 처짐, 보의 탄성 곡선 미분 방정식, 처짐 곡선 방정식 유도
1. 처짐 곡선 방정식 보에 횡하중이 작용하면 보의 축선은 구부러져 곡선으로 변형된다. 이 구부러진 중심선을 탄성 곡선 또는 처짐 곡선이라고 하며, 구부러지기 전의 중심선에서 이 탄성 곡선
nightime-mech.tistory.com
이 식을 1번 적분하면 처짐각(dy/dx), 2번 적분하면 처짐량(y)을 구할 수 있다.
위의 식을 정리하면 아래와 같이 변형이 가능하다.
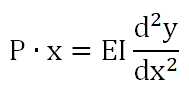
이 식을 x에 대해서 적분하면
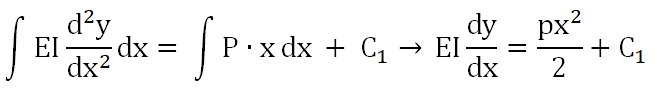
한번 더 적분하면

여기서 경계 조건 x = ㅣ에서 기울기 (dy/dx) = 0, 처짐량(y) = 0을 부여하면

이 되며, 처짐각 수식이 정리가 가능하다.

그리고 C2를 구하여서 최종 정리하면
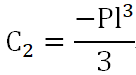
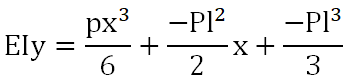
가 되며 이를 처짐량(y)에 대해 정리하면

자유단 (x=0) 최대 처짐각과, 처짐량이 일어나므로 위의 식을 정리 하면 구하고자 하는
최대 처짐각과 처짐량을 구할 수 있다.
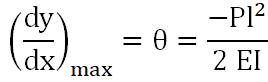

2. 균일한 분포 하중을 받는 외팔보
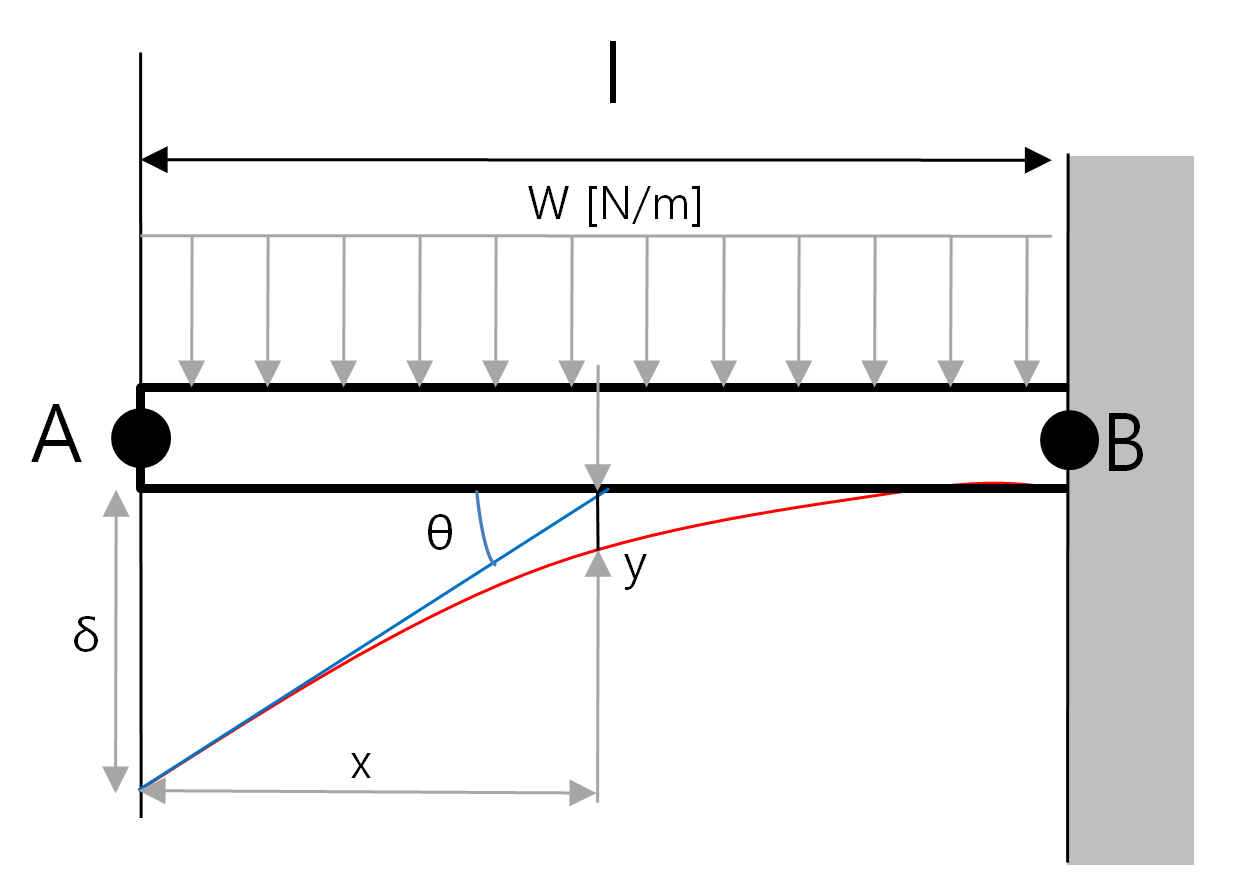
단위 길이당 하중(균일 분포하중)을 w라 할때도 집중하중과 마찬가지의 방식으로 수식을 유도하면 된다.
먼저 굽힘 모멘트 M은
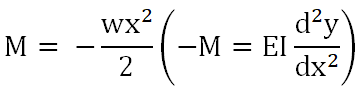
마찬가지로 처짐 식을 적분하고 적분 상수를 구해주면 최종적으로 아래와 같이 정리가 된다.