공학/Basic
벡터의 내적(Dot Product, inner product) 정의와 의미, 그리고 특징
깜장스
2023. 5. 17. 21:00
반응형
1. 벡터의 내적
내적은 두 벡터 간의 각도를 구할때 많이 사용한다.
게임에서는 내적을 이용해서 물체가 앞에 있는지, 뒤에 있는지 판별할 수 있다.
캐릭터의 시선을 기준으로 좌, 우 90도가 넘어가는 순간 코사인 값은 음수를 갖기에
벡터와 몬스터의 위치벡터를 내적해서 양수값이면 캐릭터의 정면, 음수값이면 후면에 존재한다는 뜻으로
활용이 가능하다.
이를 이용하여 시야각 내에 있는지 없는지도 확인 가능하다.
내적은 벡터를 마치 숫자처럼 곱하는 개념이으로, 방향이 있으므로 일치하는 만큼만 곱한다.
(정사영 시켜서 그 벡터의 크기를 곱하는 형태이다.)
그래서 벡터의 내적의 결과값은 벡터가 아닌 스칼라이다.
예를 들어 두 벡터의 방향이 같으면, 두 벡터의 크기를 그냥 곱한다.
두 벡터가 이루는 각이 90도일 땐, 일치하는 정도가 전혀 없기 때문에 내적의 값은 0이다.
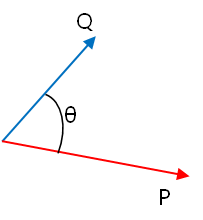
위의 그림에서 벡터의 내적은

이 곱셈은 P의 크기에 P방향의 Q 성분인 Q Cos θ 를 곱한 것 또는 Q의 크기에 Q 방향의 P 성분인
P Cos θ를 곱한 것으로 볼 수 있다. (이말인 즉! 교환 법칙이 성립된다)
그리고 내적의 정의로 부터


이 성립 되며 위에서 말한 교환 법칙과 더불어 분배 법칙도 아래와 같이 성립된다.

반응형