주파수응답함수(전달함수, FRF)로부터 강체 특성(질량중심, 관성 모멘트)을 규명하는 방법(Rigid Body Calculation with mass line) _ 1

오늘은 주파수 응답함수(FRF)로부터 질량중심, 관성모멘트 구하는 방법에 대해 알아 보겠다.

 

구조물을 자유로운 상태(free - free)로 한 다음, 충격 가진(Impact)하여 얻은 FRF (accelerance)를 이용하여 

 

강체 특성을 규명한다.

 

왜?

 

 

자유상태에서 실험을 하면 강체모드가 배제되기 때문에 일정한 값만을 가지는 수평한 직선의 주파수 응답함수(FRF)를

 

얻을 수 있기 때문이다.

 

이렇게 얻어진 수평한 직선의 우리는 질량선(mass line)이라 부른다.

 

이 질량선 값을 운동역학 방정식에 적용하면 간단한 실험으로 높은 정도의 강체 특성값 (질량중심, 관성 모멘트) 들을

 

규명할 수 있다.

 

그리고 질량을 직접 측정하여 입력함으로서 결과의 정확도를 더욱 높일 수 있다.

 

◎ 운동 방정식

 

 

 

그림에서 점F는 가진점이고, 점A, B는 응답점임.

 

점 CG는 질량중심점

 

가진점에 힘이 작용했을 때 응답점에서의 가속도간의 관계는

 

 

이를 행렬 형태로 표현하면 다음과 같다.

 

 

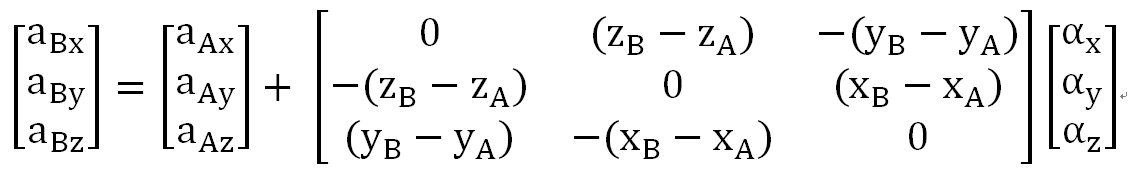
여기서 알파를 제외한 모든 값을 알기 때문에 알파의 값을 알수 있게 된다.

 

그리고 점A와 CG점에서의 응답 관계도 아래와 같이 나타낼 수 있다.

 

그리고 이는 가진력과의 관계를 통해 다음과 같이 정의가 가능하다.

 

 

 

(행렬 수식에...아랫첨자까지 만들려니 힘이드네요)

 

 

 

이렇게 정의한 행렬을 이미 알고 있는것 항과 알아내야하는 항으로 정리가 가능하며 최종적인 정리를 하면 다음과 같다.

 

이렇게 정리된 식을 보면 좌변은 모두 아는 값으로 구할수 있으며 우변에서의 CG점 좌표인 x,y,z 값만 모르니

 

이 수식을 풀수 있게 된다.

 

이렇게 해서 질량 중심의 좌표값을 알수 있게 되는 것이다.

 

다음은 관성 모멘트를 구하는 방법으로 다음 글에 계속 이어나가도록 하겠습니다.

(피곤해서 여기까지 정리합니다)