지금부터는 회귀분석(Regression)에 대해 공부를 시작해 보겠다.

============================================================================
1. 개념
◎ 매개변수 모델(parametric model)을 이용하여 통계적으로 변수들 사이의 관계를 추정하는 분석
: 독립변수가 종속변수에 미치는 영향 분석 또는 변화 예측을 위한 통계 기법 등등
◎ 영국의 유전학자 갈톤(Galton)이 두 변수 간의 상관과 회귀에 관한 분석 방법을 처음 제시.
부모와 자식들 간의 키의 상관관계를 분석해 본 갈톤은 다음과 같은 재미있는 관계를 찾아냄
특이하게 큰 부모의 자식들은 대개 크긴 하되 부모들보다는 대부분 작으며,
작은 부모들의 자식들은 대개 작긴 하되 부모들보다는 대부분 크다는 사실이다.
이러한 경향은 사람들의 키가 평균키로 회귀하려는 경향이 있음을 말하는 것인데,
바로 이 연구에서부터 회귀분석이라는 용어가 사용되게 됨.
2. 용어
① 영향을 주는 변수 : 독립변수(independent variable), 설명변수(explanatory variable)
② 영향을 받는 변수 : 종속변수(dependent variable), 반응변수(response variable)
③ 예측모델(prediction model) 또는 예측모형 : 독립변수에 해당하는 자료와 종속변수에 해당하는 자료를 모아
관계를 분석하고 이를 예측에 사용할 수 있는 통계적 방법으로 정리한 것
3. 목적
① 종속변수와 독립변수들 사이에 존재하는 함수 관계를 추정
② 독립변수들이 종속 변수에 미치는 효과를 검정
③ 추정된 회귀함수를 이용하여 종속 변수의 미래의 값을 예측.
4. 단순 회귀 모형
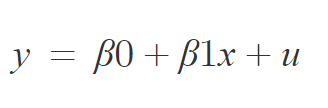
x : 독립변수
u : 오차항
5. 회귀모형에 대한 가정
① 선형성 : 산점도를 통해 확인.
② 독립성 : 잔차와 독립변수의 값이 관련되어 있지 않다.
③ 등분산성 : 오차항들의 분포는 동일한 분산을 갖는다.
분산이 일정하지 않으면, 가중 회귀를 쓰거나 종속 변수를 변화시킨다.

잔차와 예측치의 산점도가 부채꼴이면, 등분산성이 무너지고 오차항이 이분산성을 갖는다고 함.
이분산성은 독립변수 값이 변화할 때 종속변수 값들의 분산이 상이하게 될 때 나타남.
④ 비상관성 : 잔차들끼리 상관이 없어야 한다.
⑤ 정상성 : 잔차항이 정규분포를 이뤄야 한다.
6. 접합성 검증과 결정 계수
◎ 접합성 검증 : 도출한 회귀식이 표본 측정치를 얼마나 잘 설명하는지를 확인하는 것
◎ 결정 계수 : 표본에 대한 회귀선의 설명력을 확률로 표현한 계수로, 1에 근접할수록 회귀선의 추정치를
잘 반영하고 있다고 볼 수 있다.


============================================================================

